Streamlining Drug Developments Through the In Silico Approach to Ligand-Target Interactions

Significance Statement

This work deals with the In Silico models designed to optimize the drug- receptor, ligand-target, coupling fine recognition. This itself is no doubt a truly critical issue for pharmacokinetics based experimental therapy efforts, whatever medicines are the case. Being a fundamental prediction-making computational platform, this upgraded pharmacokinetic paradigm might serve to solve both general and tissue specific pharmacological and experimental ther apeutic tasks. The aim of a present study is to harmonize a broad spectrum of rather variable and controversial biomedical, computational and, last not least, purely mathematical findings and statements on this point.

Problem

Most chemical starting points for design lack the affinity required to function as drugs and optimization typically results in increased lipophilicity, molecular size and molecular complexity [1-10]. This highlights excessive molecular size and lipophilicity as primary design risk factors. Risks associated with molecular complexity [2,6,9] are more likely to be encountered in the screening phase of a project. Molecular complexity can also be seen inversely as the degree to which a compound is structurally prototypical [1,3,7] (e.g., minimally substituted) and might also be defined in terms of the molecular shape [7,10] of a compound or the roughness [8,10] of its molecular surface. Molecular recognition [1,5,9] provides much of the conceptual framework for drug design and many medicinal chemists consider molecular interactions [6,9,10] when elaborating chemical start points. While a structure-activity relationship can point to the importance of individual interactions, the contribution of a protein-ligand contact to affinity is not, in general, an experimental observable [1-9]. It would be safe to say, however, that a weak link in a row of the drug design leading events is a hard way to make a choice of the most efficient pharmacophore revealed within a paradigm of the «drug-target», i.e., «ligand-receptor », affinity docking.

To optimize a solution of this dilemma, an arsenal of mathematical methods might be employed once they’re focused on a modeling and testing of the above-mentioned phenomena. As per these methods themselves, they are still far of being perfect and yet there is «enough room ahead» to move forward with an attempt to upgrade the current probabilistic computational outlook for better In Silico ligand-receptor fitting. Even though the computational (In Silico) methods have been developed and widely applied to pharmacology hypothesis formalization and testing [11-13,20,22], this is still a kind of the “rocky path” on a way of selection of very few perfect- looking molecule candidates. However, this process could be accelerated and simplified owing to either computer - aided drug design or by means of In Silico based structure/function prediction, modeling and target validation, and pharmacokinetics/ pharmacodynamics «landscape» simulation studies [1,11-24]. These numerous and variable data provides enough information to analyses aiming to optimize the In Silico approach as a source of tools for experimental and applied pharmacology.

Bailey Differential Equation

Legible proof of Bailey’s formula [2,3,8] is presented in this work in a form suited for immediate practical use. Below t stands for time and x(t), t ≥ 0 denotes a homogeneous Markov chain with continuous time and the state space 0 N consisting of non-negative integers (the population, in the basics example considered). The process values x(t) at time 𝑡 are denoted as {x(t)}, and Δx(t) = x(t + Δt) − x(t) is the Markov process increment (the population change over the period of time from 𝑡 to 𝑡 + Δ𝑡). The probability distribution at time t is determined by the probabilities px(t) of the population numbering x(t) species at time t. The probability-generating function of the distribution for the process x(t) is given by

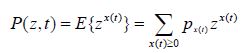
with | z | ≤1. This probability distribution expressed as the Markov related transition function might be presented here within a Markov paradigm being adopted to homogeneous Markov chain as seen from (1):

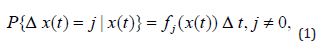
Here ki is the i-th cumulant of the x(t) process at time t ≥ 0 . The first cumulant is equal to the expected value, the second – to dispersion, and the first cross- cumulant – to covariance.

Theorem 1: Suppose the above homogeneous Markov chain x(t) , t ≥ 0 with continuous time and with the state space 0 N is defined and its generating function M(θ ,t) is differentiable. Then the generating function of the homogeneous Markov process is governed by the equation

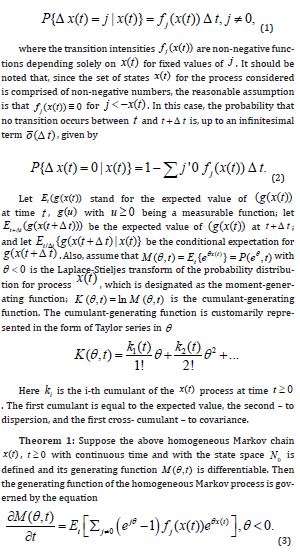
Proof: 1. Assuming that all of the expected values implied below exist, the expected value obeys the relation

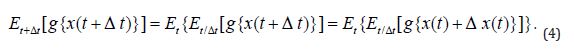
Given the above and as long as the expected values exist and the process is of the Markov type, the moment-generating function for the process x(t) , t ≥ 0 at time t + Δ t can be written with the help of (Equation 4) as

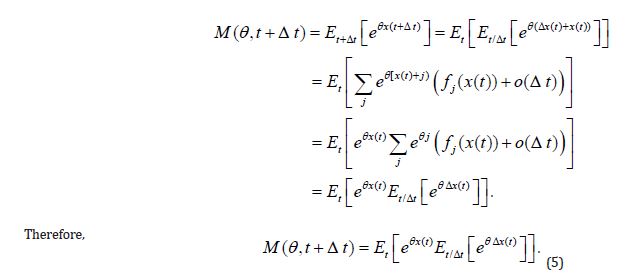
2. Consider the following limit

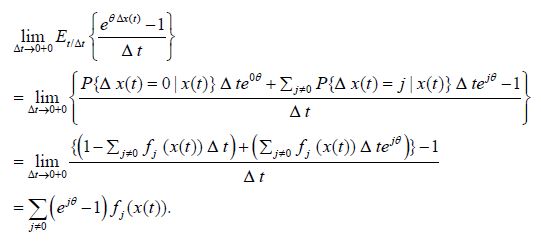
Thus,

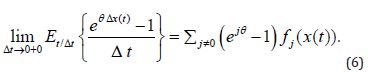
3. The derivative of the moment-generating function exists and

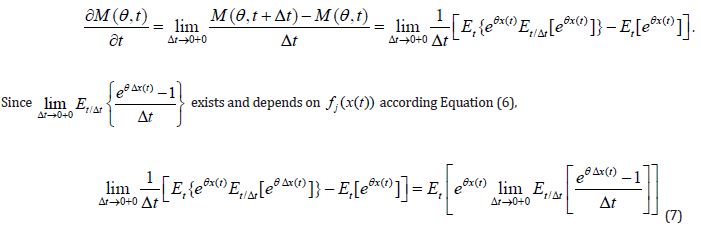
Theorem 1 follows from (Equations 6&7).

Theorem 2: If, for the above homogeneous Markov chain with x(t) , t ≥ 0 , with continuous time, and with the state space N₀ , the functions f_j(x(t)) can be presented as polynomials of the form

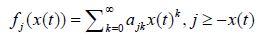
and if the derivatives implied below exist, the following differential equation holds true

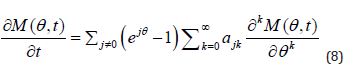
Proof: Taking into account that

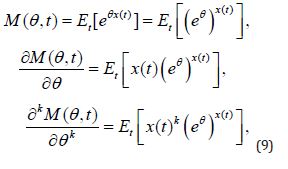
(Equation 1&3) can be cast in the form

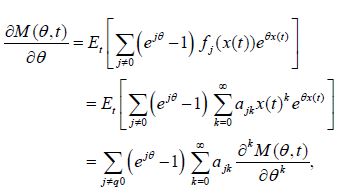
which proves the theorem.

Theorem 3: If, for the above homogeneous Markov chain with x(t) , t ≥ 0 , with continuous time, and with the state space N₀ the functions f_j(x(t)) can be presented as polynomials of the form

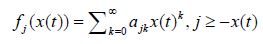
and if the derivatives implied below exist, the following differential equation holds true

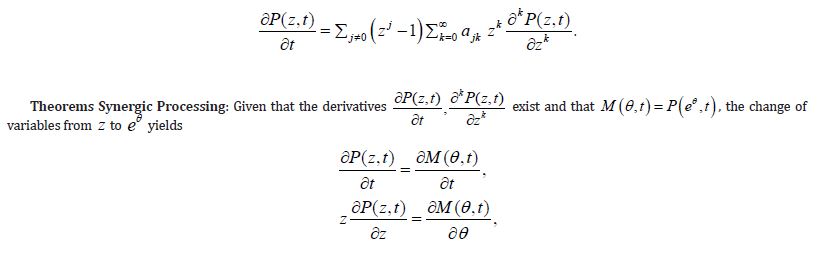
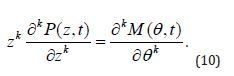
To come closer to result proposed by Theorem 2, the (Equation 8) should be just substituted with (Equations 1-10) so the requirements of Theorem 2 become perfectly met. The practical applications of the above differential equations are examined below.

Application of Outcoming Algorithms

Bailey’s Equation in Kinetics Analysis

First-Order Elementary Chemical Reaction

Suppose that the process of decay of substance A paralleled by the generation of substance B evolves with the probability α per molecule:A Bα→. The process is described by the function f −1 = αt, and Bailey’s equations become

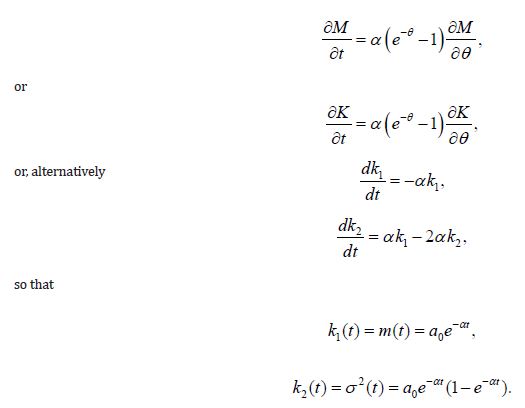
Here a₀ is the initial concentration of A , assuming that the initial dispersion of A is zero.

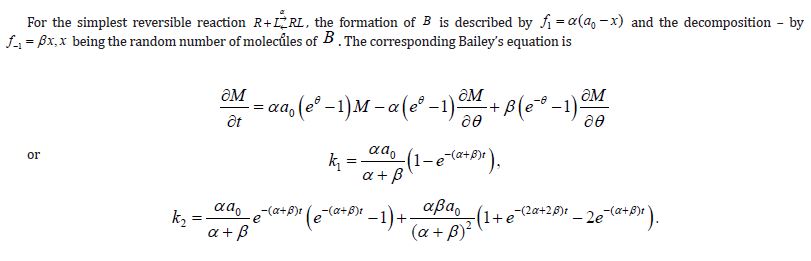
Ligand-Receptor Interaction

Pharmacokinetic Outlook

A classical single-compartment pharmacokinetic model designed for an oral drug administration might by simplified as this (11):

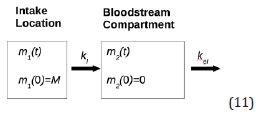
In the (Equation 12), m₁(t) stands for the drug mass at the intake point, m₂(t) means the drug mass in blood circulation system, while K1 and K2 are administration elimination rates, respectively:

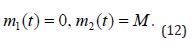
The law of mass action for scheme (11) and (Equation 12) is

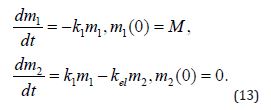
The solution to the above set of equations is

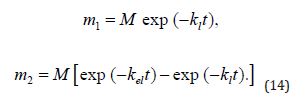
An analogous set of equations for a drug directly injected into the bloodstream is

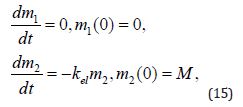
its solution trivially being

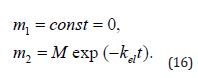
The forms of the solutions to (Equation 13&14) are impractical, considering that the drug concentration in the bloodstream rather than its total mass is typically measured experimentally. (Equation 13&14) can be conveniently transformed using the fact that drug concentration C and mass m are related as

where the total blood volume is V . Taking into account an assumption that the drug is not an active diuretic agent, i.e., that V = const - 5L , the following combination of (Equation 14&17) arrives to:

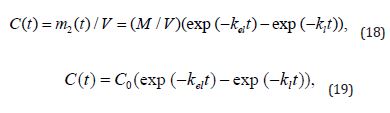
where C(t) is the time-dependent drug concentration in the bloodstream and C₀ is a constant denoting its initial effective concentration? However, once the drug administrated in a single i.v. injection, the solution is more laconic as compared to (Equation 18&19):

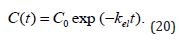
This shows a monotonous trend in the blood drug concentration time-dependent decrease. Noteworthy, a known interaction of drug molecules with the blood plasma proteins is to be treated as described in (Equation 21):

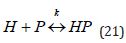
where H is the drug, P is the blood protein, HP is their complex, and k is the dissociation constant? The drug concentration generally tends to be much lower than that of the blood proteins. For example, the concentration of albumin, which is the key binding blood protein, is 10⁻⁵M while the concentration of the nerve growth factor only reaches 10^{−9sup> −10−1sup>1M [25, 26]. The concentration of the growth hormone is 0.5 − 2.0 nM [27, 28] while the concentration of the binding protein is 1.5 mM [25-28]. Therefore, the concentration of the drug-blood protein complexes for scheme (21) is}

where 0 [H ] is the initial concentration of the drug? For most drugs, K >>[H] and, accordingly, (Equation 22) becomes

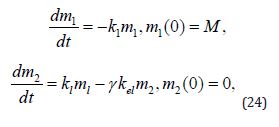
where β is the binding constant? The value β =1 means that the drug undergoes no binding with blood proteins, and β = 0 shows that all drug molecules are drawn into association with blood proteins.

It may be the case that only bound drug (e.g. bilirubin) or only unbound agent (e.g. sex steroids) is excreted. In this situation, (Equation 23) is rewritten as

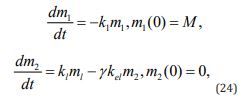
where γ is a constant such that γ =α if only the bound form of the drug is excreted and γ = β in the opposite case. The solution to (Equations 14-24) is

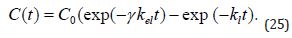
It should be noted that the underlying assumption in the analysis of biological effects which are due to the evolving drug concentration on the basis of (Equations 14-25) is that only the free form of the drug triggers response.

Ligand Efficiency and Molecular Dynamics

Compound-level efficiency metrics are typically constructed by either scaling (i.e., divide affinity by risk factor) or offsetting (i.e., subtract risk factor from affinity) [2-7]. LE was introduced [1, 8, 25] as a metric to normalize affinity with respect to molecular size by scaling the standard free energy of binding, ΔGO , by the number, N_nH , of non-hydrogen atoms (the term heavy atoms are also used) in the molecular structure as follows:

The standard state was not specified when the LE metric was introduced although it appears to be widely believed [23] that must be set to 1M for calculation of LE. The Achilles heel of the LE metric is its nontrivial dependency [29] on C^o and, as conventionally [3,7] defined, LE has a 1M concentration unit built into it. As noted in [5,6,30] the choice of a particular value ofCo , such as 1M , to define the standard state is entirely arbitrary and a requirement that C^o only take a specific value cannot be accommodated within the framework of thermodynamics. Drug discovery scientists need to be wary of correlation inflation [3-8,31] which can be loosely defined as presentation or analysis of data in any way that makes trends appear to be stronger than they actually are.

The relevance of data must also be considered when using physicochemical characteristics such as molecular size to assess risk. For example, an activity threshold [4, 24] of > 30% inhibition at 10μM for promiscuity analysis is not especially relevant if considering the likelihood of off-target effects for a drug with a peak unbound plasma concentration of 100 nM . Sample bias can be significant, even in large datasets, as exemplified by divergent conclusions of two apparently similar studies [7,10] with respect to the relationship between pharmacological promiscuity and molecular size. The observation that averages molecular weight appears to decrease [1,9] with promiscuity is particularly relevant to the use of LE because promiscuity would generally be considered [8,32-34] to be an undesirable characteristic for a compound.

Thermodynamics Aspects of Ligand-Protein Association

The LE metric [4-10] was introduced in thermodynamic terms and it is sometimes believed that it measures the degree to which molecular interactions between ligand and target are optimal. The standard free energy of binding, ΔGO , [7, 10] can be written in terms of the gas constant (R), thermodynamic temperature (T), C^o and the equilibrium concentrations of protein ([P]), ligand ([L]), and protein-ligand complex ([P.L]):

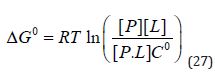
(Equation 27) shows that ΔGO is a function of C^o and this is one reason that values of standard free energy of binding should not be termed absolute. By convention, C^o is taken to be 1M although, this is arbitrary and the value of C^o has no physical significance [6-9]. In some situations, the dissociation constant, D K , is defined to be equal to the argument of the logarithm in equation (27) and is therefore dimensionless. D K values are conventionally quoted in units of concentration and (Equation 27):

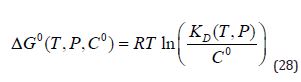
(Equation 28) shows that a tenfold increase in C^o leads to a decrease in ΔGO of 1.36 kcal/mol at 298 K. The sign of ΔGO has no special significance and simply indicates whether or not D K is greater or less thanCo . The dependence of ΔGO on Co is a consequence of the stoichiometry of association of ligand with target and ΔGO for formation of a ternary complex (relevant when considering the thermodynamic consequences of fragment linking) will exhibit a different dependence on Co to ΔGO for a binary complex. The stoichiometry corresponding to a ΔGO value is specified by the change, ΔN , in the number of species for the corresponding reaction and it can also be seen as a ‘hidden dimension’ ofΔGO . For example, formation and dissociation of 1:1 complex has ΔN values of –1 and +1 respectively. The value of ΔN determines the dimensions of the corresponding equilibrium constant:

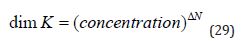
The dependence of ΔGO on C^o is a consequence of the loss of translational entropy resulting from association and it has two important implications. First, ratios of ΔGO values also depend on C^o even though the ratios themselves are dimensionless and ΔGO values should therefore be compared as differences (i.e.,ΔΔG ). Second, if a free energy change is written as a sum of free energy changes, then the sum needs to have the same dependency on C^o as the original free energy change since the equality must hold for all values of C^o . This is equivalent to requiring that the sum of ΔN values for the components of a free energy decomposition be equal to the ΔN value for the free energy change that is decomposed.

One way in which stoichiometry can be accounted for in free energy decompositions is to associate each free change with its corresponding ΔN value using square brackets. The study on attribution and additivity of binding energies can be used to illustrate this: the intrinsic binding energy for a group X as the difference in ΔGO for compounds in which X is present (AX ) or absent (A) in the relevant molecular structures:

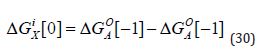
The intrinsic binding energy is associated with a zero value of ΔN and is therefore independent of C^o . It shows the ΔGO value for a compound with linked groups A and В in its molecular structure as the sum of the intrinsic binding energies of A and B, and the “connection Gibb’s energy” (ΔG^S ) :

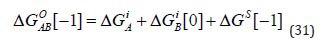
(Equation 31) is particularly relevant to fragment linking and it is important to note that ΔGS does depend on Co [1, 2]. In some studies, ΔGO is decomposed into a value corresponding to zero molecular size 0 ( ) MS G = Δ and a ΔΔG value [5, 9]:

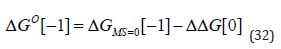
One general approach to modelling affinity is to use (Equation 33) in which ( 0) i A i > is a parameter associated with the substructure i and ni is the number of occurrences of that substructural element:

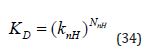
The A0 term has the same dependency on Co as ΔG^O and its inclusion in (Equation 33) allows changes in concentration unit to be easily accounted for. The substructures are typically groups at substitution sites on a scaffold and the ni values are either 1 or 0 and A0 may correspond to the affinity of the unsubstituted scaffold. Schemes for decomposition of ΔG^O based on (Equation 33) cannot be considered to be group additive because of the presence of the A₀ term which is not associated with any group. An equivalent way to examine the stoichiometry issue is to consider the implications of writing K _D as follows where k_nH corresponds to Δg as defined in (Equation 26):

An example of a non-local effect would be substitution at one position of a molecular structure preventing a substituent at another position from forming optimal interactions with the target. When interpreting binding thermodynamics in terms of molecular interactions, it should always be kept in mind that intermolecular contacts (e.g., between unbound ligand and solvent) that are not present in the protein-ligand complex also influence ΔH and ΔS^O .

Perception of Affinity Varies with Concentration Unit

Some of the problems that result from using LE as a design metric can be seen more clearly if it is expressed using a base 10 logarithm and without energy units:

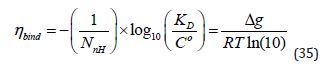
The quantity n_blindrelated to Δg by a multiplicative factor of RT ln(10) that is independent of C^o and therefore both quantities and therefore both quantities respond in an identical manner to a change in C^o . One rationale for using n_blind is that drug discovery scientists typically use pIC₅₀ or PKD rather than ΔG^O in «drug-target» analysis. The quantity n_blind is also related to ligand efficiency by atomic number (LEAN) that is calculated by scaling pIC₅₀ by N_nh Unlike LEAN, n_blind C⁰to emphasize this. Although standard state conventions do not apply to potency measures such as IC₅₀and EC₅₀which are usually quoted in μM or nM , potency must still be scaled by a concentration value for the logarithm calculation because the logarithm function is not defined for dimensioned quantities.

Using n_blind rather than ΔG# reinforces the point that the problems associated with LE are due to the mathematical behavior of the logarithm function. While the use of a concentration unit other than 1 M to define LE is unusual, there certainly is precedent for doing so. LE is used to specify affinity cutoffs as a function of molecular size and a Δg value of 0.3 kcal/mol per non-hydrogen atom has been suggested [6,10]. Specification of affinity cutoffs in this manner forces the line defining acceptable affinity to intersect the affinity axis at a point corresponding to a D K value of 1 M. The minimum Δg value of 0.12 kcal/mol per non-hydrogen atom recommended can be translated (C^o =1M; T = 300 K) to pK_D values corresponding to the lower (700 ; 50) nH Da N ≈ and upper (3000 ; 214) Da N_nH ≈ limits. The lower ( 4.4) D pK = of these two values would not appear to be a useful design criterion while the higher value ( 18.7) D pK = would not generally be measurable.

In general, affinity thresholds should be specified directly and LE should only be used for this purpose if supported by the data. LE features prominently in the literature of fragment-based lead discovery [7,32,33] to the extent that it is sometimes presented as an important rationale for screening fragments. Comparison of LE values for fragment hits and the corresponding leads can be seen as an attempt to quantify how effectively an increase in molecular size translates to affinity. This is still a valid objective even though the LE metric would appear to be unfit for this purpose. The most obvious way to do this is to scale Δ_p Δ _D by ΔN_nH :

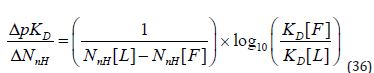
Using ΔpK _D(the logarithm of a ratio of K_D values) eliminates the dependency on C_o that makes bind Δη (and Δg ) unsuitable for comparison of start and end points for projects. An additional benefit is that ΔpKD is likely to be relatively insensitive to the approximation of D K by 50 IC . This approach to assessing optimizations has precedent [4] and reported that a tenfold improvement in D K corresponded to a mean

increase in molecular weight of 64 Da (standard deviation = 18 Da) for 73 compound pairs. Some other reports [3,8,10] also illustrates the benefit of observing the response of affinity to an increase in molecular size directly rather than indirectly by using the LE metric. It can be useful to compare the changes in affinity and lipophilicity that result from structural elaboration and one way of achieving this is to offset the change in affinity by change in lipophilicity:

The notation [X →Y] can be used to specify structural transformations and to indicate that a change in the value of a property such as ΔGO , D pK or nH N has been calculated by subtracting the value of the property for compound X from that for compound Y. The definition of GE expresses (Equation 36) in terms of free energy rather than dissociation constant and (Equation 37) could be used in an analogous manner to specify the efficiency of substitutions from the perspective of lipophilicity. The fundamental difference between the two metrics is that GE is independent of Co because it is defined in terms of ΔΔG . Although GE is sometimes presented as a substructural property, it is actually structural transformations (e.g., substitute hydrogen with chlorine) with which values of GE should be associated. The ΔΔG values used for calculation of GE cannot generally be interpreted as substructural contributions to affinity because summation of values of ΔΔG (ΔN = 0) cannot reproduce the dependency of ΔGO (ΔN = −1) on C^o .

Limitations in Ligand Affinity

It is important to stress that residuals are not generated in isolation and they result from analysis that, arguably, should be performed anyway. The line fit to a plot of affinity against molecular size is likely to be a better predictor of outcome than a line that has been artificially forced to intercept the affinity axis at a point corresponding to a D K value of 1 M. The strength of the trend also provides an indication of how useful normalization of the data is likely to be. In an optimization project, a relatively weak correlation between affinity and molecular size may point to the extent that it cannot be adequately explained by molecular size alone. Here, it should be pointed out again that the attempts to employ an In Silico research for the ongoing drug developments are growing [2,4,7,11- 22].

Thus, virtual ligand screening, ligand - target affinity prediction, drug target/ lead finding, pharmacophore and medicinal compounds library formation are no doubt promoted by a variety of computational approaches [14,15,20-22]. Particularly, databases, pharmacophore, profiling, molecular homology models, quantitative structure- activity links, computer algorithms for data treatment are the examples of In Silico techniques we might be interested in [11-13,16,18,19]. These techniques are to be used in conjugation with in vitro data to create models that provide insight into pharmacokinetics platforms [14,15,17,21,22]. This, as a whole, might help to find out, characterize and predict the optimum drug administration outcomes for individuals with similar genotypes/ phenotypes [11-22].

A neglected Baileyan computational approach is now modified to renovate and improve the In Silico pharmacokinetic modeling suitable for either preclinical trail planning or the drug- receptor docking scenario analysis. This was found a promising research tool for the «drug-target» interaction analysis required by a contemporary drug design paradigm. Virtual In Silico screening, particularly the one based on a semi-forgotten Baileyan systematic analysis, may help to reduce the number of candidate molecules to a smaller set of the best ones that are further checked out experimentally within a short but efficient track. This rational way would make drug development more goal- oriented and, therefore, saves time and funds.

The authors declare that no funds, grants, or other support were received during the preparation of this manuscript.

The authors declare that there is no conflict of interest regarding the publication of this paper.

As per the ethics approval statement, funding information and the competing interests, these matters are clearly specified above. All Authors are perfectly agreed on their unambiguous consents with both participation in this work and with a further publication of its content, results and conclusions.

This article contains no datasets generated or analyzed during the current study.

Authors are grateful to Dr. Santiago Camacho (Dept. Mathematics and Computer Science, Wesleyan University - Bloomington, IL) for stimulating comments on preliminary findings.

1. Muro S (2012) Challenges in design and characterization of ligand - targeted drug delivery J Control Release 164(2): 125-137.
2. Wang Y, Zeng J (2013) Predicting drug-target interactions using restricted Bolzman machines. Bioinformatics 29(13): 126-134.
3. Pawson AJ, Sharman JL, Benson HE, Faccenda E, Alexander SPH, et al. (2014) The IUPHAR/BPS Guide to pharmacology: an expert-driven knowledge base of drug targets and their ligands. Nucleic Acids Res 42(D1): D1098-D1106.
4. Salahudeen MS, Nishtala PS (2017) An overview of pharmacodynamic modelling, ligand-binding approach and its application in clinical Saudi Pharm J 25(2): 165-175.
5. Li D, Ji B (2019) Protein conformational transitions coupling with ligand interactions: simulations from molecules to medicine. Medicine in Novel Technology and Devices 3(6): 100026-100038.
6. Holze J, Bermudez M, Pfeil EM, Kauk M, Bodefeld T, et al. (2020) Ligand-specific allosteric coupling controls G-protein-coupled receptor signaling. ACS Pharmacol Transl Sci 3(5): 859-867.
7. Zhu S, Wu M, Huang Z, An J (2021) Trends in application of advancing computational approaches in ligand Exp Biol Med 246(9): 1011-1024.
8. Farinde A (2022) Drug - Receptor South California University Press: Orange Beach CA.
9. Le J (2022) Overview of Pharmacokinetics, University of California ; San Diego, CA.
10. Saurabh S, Nadendla K, Purohit SS, Sivakumar PM, Cetinel S (2023) Fuzzy drug targets: disordered proteins in the drug-discovery realm. ACS Omega 8(11): 9729-9747.
11. Brogi S, Ramalho TC, Kuca K, Medina-Franco JL, Valko M (2020) Editorial: In silico Methods for Drug Design and Discovery. Front Chem 8:
12. Shaker B, Ahmad S, Lee J, Jung C, Na D (2021) In silico methods and tools for drug discovery. Comput Biol Med 137: 104851.
13. Chang Y, Hawkins BA, Du JJ, Groundwater PW, Hibbs DE, et al. (2022) A Guide to In Silico Drug Pharmaceutics 15(1): 49.
14. Sadybekov AV, Katritch V (2023) Computational approaches streamlining drug discovery. Nature 616(7958): 673-685.
15. Roney M, Fasihi Mohd Aluwi MF (2024) The importance of in-silico studies in drug discovery. Intelligent Pharmacy 2(4): 578-579.
16. Berkley K, Zalejski J, Sharma N, Sharma A (2025) Journey of PROTAC: From Bench to Clinical Trial and Beyond. Biochemistry 64(3): 563-580.
17. Li Z, Zeng Y, Jiang M, Wei B (2025) Deep Drug-Target Binding Affinity Prediction Base on Multiple Feature Extraction and ACS Omega 10(2): 2020-2032.
18. Ortega-Vallbona R, Johansson L, Carpio LE, Serrano-Candelas E, Mahdizadeh SJ, et al. (2025) Computational Characterization of the Interaction of CARD Domains in the Apoptosome. Biochemistry 64(2): 401-418.
19. Brożek A, Theodoris CV (2025) AI learns from chromatin data to uncover gene interactions. Nature 637(8047): 799-800.
20. Puentes PR, Rueda-Gensini L, Valderrama N, Hernández I, Gonzalez C, et al. (2022) Predicting target–ligand interactions with graph convolutional networks for interpretable pharmaceutical discovery. Sci Rep 12(1): 8434.
21. Shaikh F, Tai HK, Desai N, Siu SWI (2021) LigTMap: ligand and structure-based target identification and activity prediction for small molecular compounds. J Cheminform 13(1): 44.
22. Fatoki TH, Balogun TC, Ojewuyi AE, Omole AC, Olukayode OV, et al. (2024) In silico molecular targets, docking, dynamics simulation and physiologically based pharmacokinetics modeling of oritavancin. BMC Pharmacol Toxicol 25(1): 79.
23. Zastrow M (2017) Drug Receptors & Pharmacokinetics. PP: 260-
24. Yang D, Zhou Q, Labroska V, Qin S, Darbalaei S, et al. (2021) G protein - coupled receptors: structure – and function-based drug Signal Transduct Target Ther 6(1): 7.
25. Braga E, Baik H, Lee D, Sturmer R, Heuer J, et al. (2020) Synthesis of human TFF1, its homodimer provides novel insights into mechanisms of Chemical Communications 56(47): 6420-6423.
26. Muttenhaler M, King GF, Adams DJ, Alewood PF (2021) Trends in peptide drug discovery. Nat Rev Drug Discov 20(4): 309-325.
27. Angelopoulou E, Pyrgelis ES, Piperi C (2022) Emerging potential of the Phosphodiesterase PDE inhibitor ibudilast for neurodegenerative diseases: an update on preclinical and clinical evidence. Molecules 27(23): 8448-8454.
28. Sijben HJ, Superti-Furga G, Jjzerman AP, Heitman L (2022) Targeting solute carriers to modulate receptor - ligand interactions. Trends i Pharmacological Sciences, 43(5): 358-361.
29. Bazzari FH, Bazzari AH (2022) BACE1 inhibitors for Alzheimer's Disease: the past, present and any future? Molecules 27(24): 8823-8832.
30. Lazewska D, Olejarz-Maciej A, Reiner D, Kaleta M, Latacz G, et al. (2020) Dual target ligands with 4- tert- Butylphenoxy Scaffold as Histamine H₃ receptor antagonists and monoamine oxidase B inhibitors. Int J Mol Sci 21(10): 3411-3418.
31. Poongavanam V, Kolling F, Giese A, Goller AH, Lehman L, et al. (2023) Predictive modeling of PROTAC cell permeability with machine learning. ACS Omega 8(6): 5901-5916.
32. Babcock JJ, Li M (2013) Inside job: ligand-receptor pharmacology beneath the plasma Acta Pharmacol Sin 34(7): 859-869.
33. Nasser TA, Adel R, Badr A, Teleb M, Bekhit AA, et al. (2023) Combined cancer immunotheranostic nanomedicines: delivery technologies and therapeutic outcomes. ACS Omega 8(5): 4491-4507.
34. He You CZ, Jiang HL, Jiang Y, Xu HE, et al. (2023) AlphaFold2 versus experimental structures: evaluation on G protein-coupled receptors. Acta Pharmacologica Sinica 44(1): 1-7.