 Conceptual Paper
Conceptual Paper
Sequential Decomposition Algorithm of Blocking the Selected Edges in the Digraph
Institute for Applied Mathematics FEB RAS, Russia .
Received Date: October 28, 2019; Published Date: November 04, 2019
Abstract
In this paper, a protein network represented by a directed graph is considered. The problem of determining the minimum number of edges that break paths from the input proteins of the network to the output ones and passing through some subset of proteins in this network is analyzing. A sequential decomposition algorithm, basing on a selection of classes of cyclically equivalent nodes in the sub-graphs with dedicated subset of nodes and on a construction of some bipartite graph is suggesting. This algorithm increases significantly previous results obtained in [1,2].
Keywords: Cluster; Digraph; Sub-graph; Protein network; Connectivity component
Introduction
Our task is to determine the number of edges that allow blocking unwanted nodes in a directed graph (digraph). Consider a digraph G with a set of nodes U. Let a subset U/ ⊆U of socalled undesirable nodes. Our task is to construct an algorithm for allocating a set of edges, removal of which from the digraph G leads to blocking (breaking) all paths entering the set U/ from the outside and leaving the set U/ outside.
This problem is NP- problem, but if you can somehow split the digraph G into sub graphs, it is possible to reduce the number of edges removed and to simplify the calculations by solving this problem for the selected sub-graphs. Indeed, denote p (denote q ) the total number of edges coming from the set U \U/ to the set U/ (coming from the set U/ to the set U \U/ . Then you can only delete edges whose number is less. Moreover, splitting the digraph into sub-graphs we reduce the total number of deleted edges.
Solution of the Problem
In [1], a digraph G/ is constructing of nodes from the set
U/ and the edges between them.On the set of nodesU/in [2]
the cyclic equivalence relation  is
introduced if in G/ there exists a cycle containing a,b (there exists
a path from node a to node b ). Call the cyclic equivalence classes - clusters, extending the partial order relation ≥ to clusters, and
draw between any clusters A, B an edge if such an edge exists in
G/ .
is
introduced if in G/ there exists a cycle containing a,b (there exists
a path from node a to node b ). Call the cyclic equivalence classes - clusters, extending the partial order relation ≥ to clusters, and
draw between any clusters A, B an edge if such an edge exists in
G/ .
Define the set of clusters W*(the set of clusters W** ) in which in the digraph G edges income from outside G/ (from which edges come outside G/ ). We draw generalized edges → from clusters A∈W* into clusters
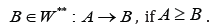 The resulting bipartite digraph is
denoting by Γ .
The resulting bipartite digraph is
denoting by Γ .
Eliminate the orientation of the edges → in the digraph Γ and
select the components of connectivity in the resulting undirected
graph, and then restore the orientation of the edges in them and get
digraphs 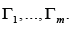
For each digraph Γt define 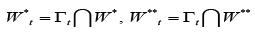 and denote Pt,qtthe numbers of edges of the digraph G , entering
from outside and leaving outside the digraph Γt respectively,t =1,...,m.
and denote Pt,qtthe numbers of edges of the digraph G , entering
from outside and leaving outside the digraph Γt respectively,t =1,...,m.
For each digraph, Γ twe remove those edges, which number is less,and we receive in equality
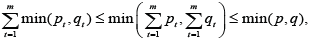 reinforcing the results of [1,2] significantly, because from the condition
reinforcing the results of [1,2] significantly, because from the condition 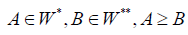 it follows that the clusters
it follows that the clusters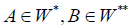 are included in the same sub graph Γt of thedigraph Γ .
are included in the same sub graph Γt of thedigraph Γ .
Supported by Russian Fund of Basic Research’s, project 17-07- 00177.
Acknowledgement
None.
Conflict of Interest
No conflict of interest.
References
- G Sh Tsitsiashvili (2019) Improved algorithm of blocking the selected nodes in the digraph, Annals of Biostatistics and Biometric Applications 3(3): DOI: 10.33552/ABBA.2019.03.000561.
- G Sh Tsitsiashvili (2019) Decomposition Algorithms of Blocking the Selected Edges in the Digraph. Annals of Biostatistics and Biometric Applications 3(3): DOI: 10.33552/ABBA.2019.03.000562.
-
Tsitsiashvili Gurami. Sequential Decomposition Algorithm of Blocking the Selected Edges in the Digraph. Annal Biostat & Biomed Appli. 3(3): 2019. ABBA.MS.ID.000564.
Cluster, Digraph, Sub-graph, Protein network, Connectivity component, Problem Statement, Applied Mathematics.
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.






