 Review article
Review article
Sauleh Distribution with Statistical Properties and Applications
Ahmad Aijaz1*, Afaq ahmad2 and Rajnee tripathi3
1, 3Department of Mathematics, Bhagwant University, India
2Department of Mathematical science, IUST, Awantipoora, India
Ahmad Aijaz, Department of Mathematics, Bhagwant University, India.
Received Date: April 5, 2020; Published Date: June 19, 2020
Abstract
The aim of this paper is to suggest a new lifetime distribution named as “Sauleh distribution”. Its various statistical and mathematical properties has been discussed including the shapes of pdf and cdf , moments, moment generating function, mean deviations , Bonferroni and Lorenz curves, order statistics and reliability analysis. The parameter of the distribution is estimated by using the famous method maximum likelihood estimation.
Keywords: Moments; Mean Deviation; Maximum Likelihood Estimation; Reliability; Order Statistics.
Introduction
Lindley [1] introduces one parameter distribution in the context of Bayesian statistics, as a counter example of fiducial statistics. In recent years, researchers have done lot of work on Lindley distribution and they have proposed many distributions of one parameter as well as of two parameters for modeling life time data. From biomedical and engineering point of view, some of these data provide good results and considered as life time distribution.
Ghitney [2] provided a comprehensive account of statistical properties of Lindley distribution and proved that it performs better than exponential distribution in many ways. They have also shown that the shape of the harzad rate function of the Lindley distribution is an increasing function and the mean residual life function is a decreasing function of the random variable. Recently Shanker [3] introduced a life time distribution named Akash distribution, which can be seen as modification of one parameter Lindley distribution.it has been applied on biological data and mentioned the superiority over exponential and Lindley distribution. Shanker [4-6] study various lifetime data from biomedical science and en gineering prospect and derived several distributions one of them is named as Ishita. K.k.shukla [7] proposed a new life time distribution named as Pranav distribution and studied its various structural properties. There are various situations where these life time distributions are not providing better fit either from theoretical or applied point of view.
Therefore, there is scope for searching new lifetime distribution which is more flexible than Lindley, Exponential, Ishita, Shanker, Pranav and Akash distribution, it has been described as.
One parameter distribution having parameter is defined by its pdf.
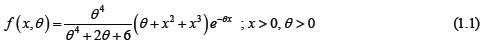
The pdf would call “Sauhleh Distribution” which is a mixture of two – distributions, Exponential distribution having scale parameter and gamma distribution having shape parameter 4 and scale parameter with their mixing proportion
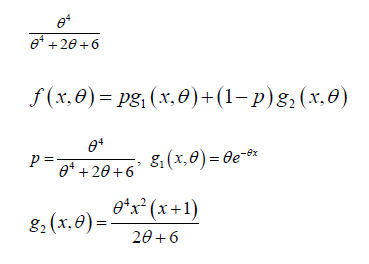
Where
The corresponding cumulative distribution function (cdf) of (1) is given as
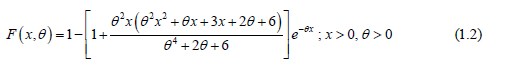
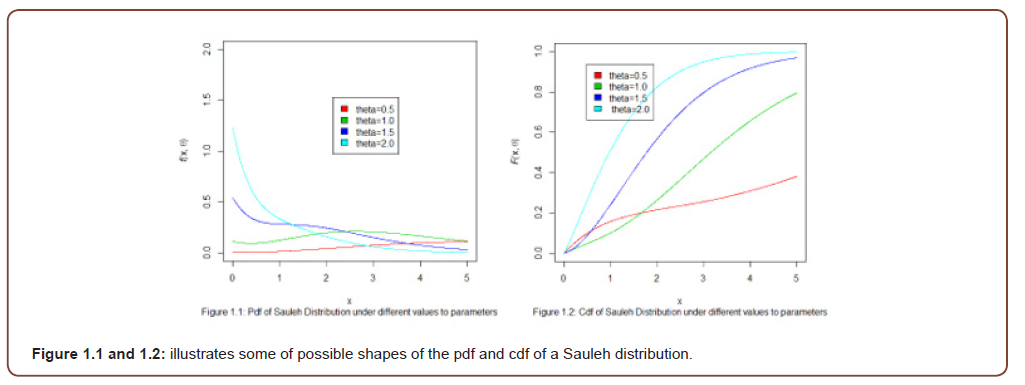
Figure 1.1 and 1.2, illustrates some of possible shapes of the pdf and cdf of a Sauleh distribution.
Moments of Sauleh Distribution
Suppose X is a random variable fallowing Sauleh distribution with parameter, then the rth moment for a given probability distribution is given as
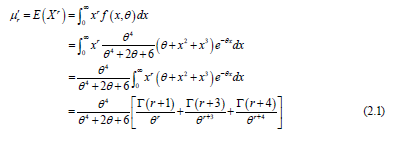
Substituting we get the first four central moments as.
For in equation (2.1), we get the mean of the sauleh distribution which is given as.
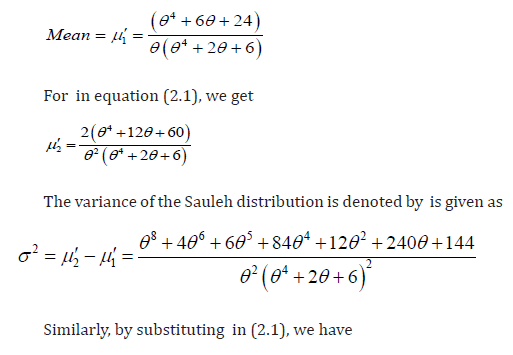

Skewness and Kurtosis of Sauleh Distribution
Skewness: it is defined as the measure of symmetry, or more
precisely the lack of symmetry of tails(about mean) of a distribution .the formula for calculating skewness of the distribution in terms of moments gave by karl pearson is described as 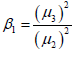
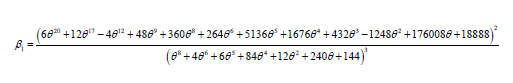
Kurtosis: it is defined as a measure of “tailedness” of the density curve .the formula for calculating the kurtosis of a distribution in terms of moments is given as.
Similarly using therelation 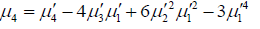
we can easily calculate 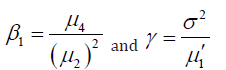
Moment Generating Function of Sauleh Distribution
Suppose X is a random variable fallowing Sauleh distribution with parameter, then the moment generating function for X denoted by is given as
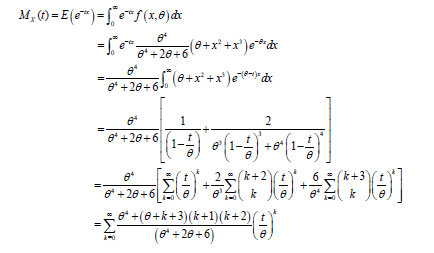
Mean Deviation of Sauleh Distribution
The amount of spread in a population is evidently measured to some extent by the totality of the deviations. Suppose x be a random variable from Sauleh distribution with mean then the mean deviation from mean is defined as
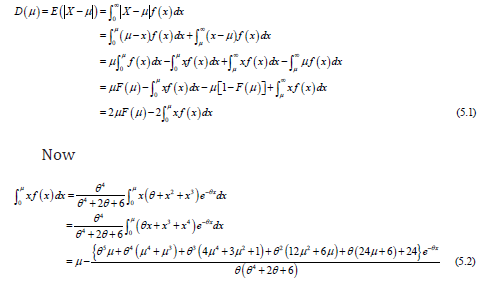
Using(5) in (1), we get
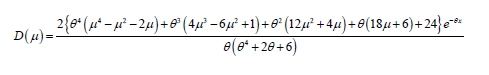
Mean Deviation From Median
Suppose x be a random variable from Sauleh distribution with median then the mean deviation from median is defined as
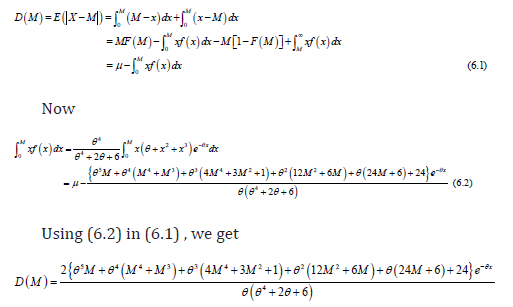
Bonferroni and Lorenz Curves
In economics the relation between poverty and economy is well studied by using boneferoni and lorenz curves [8]. Besides that these curves have been used in different fields such as reliability, insurance and biomedicine.
The bonferroni curve, is given as
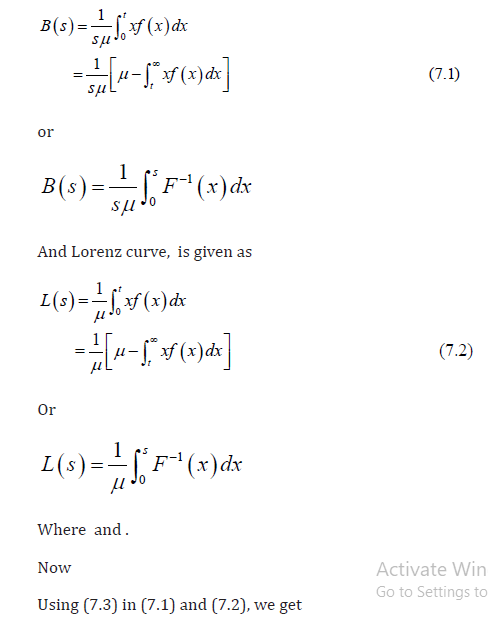
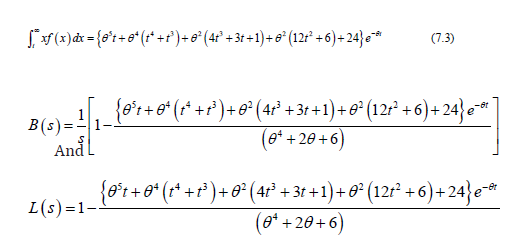
Reliability Analysis
In this section we determine two important functions reliability and hazard function of the distribution.The reliability function is also called survival function. It is defined as the probability that a system survives beyond a specified time. The reliability of a random variable x is given as.
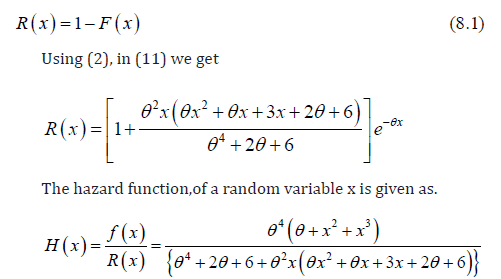
Order Statistics
Suppose be a random samples of size n from the sauleh distribution with pdf cdf .then the probability density function of order statistics is given as.

Estimation of Parameters of Sauleh Distribution
The estimation of parameters of Sauleh distribution is doing by using the method of maximum likelihood estimation. Suppose be random samples of size n from Sauleh distribution. Then the likelihood function of Sauleh distribution is given as.

Data Analysis
In this section, we provide an application of the Sauleh distribution to real data set. We use the previous data set to we obtain the ML estimates for the parameters of each model and then associating the results within goodness-of-fit statistics AIC (Akaike information criterion), AICC (corrected Akaike information criterion), and BIC (Bayesian information criterion). The amended model corresponds to smaller AIC, AICC, and BIC values. The bettor model is having lesser [9, 10] AIC, BIC and AICC values. associate the fit of the new model, Sauleh distribution with the Parnav, Akash, Ishita and Lindley distribution. First Data 1: The data set represents the survival times (in days) of 72 guinea pigs infected with virulent tubercle bacilli, observed and reported by Bjerkedal (1960). The data are as follows:0.1, 0.33, 0.44, 0.56, 0.59, 0.59, 0.72, 0.74, 0.92, 0.93, 0.96, 1, 1, 1.02, 1.05, 1.07, 1.07, 1.08, 1.08, 1.08, 1.09, 1.12, 1.13, 1.15, 1.16, 1.2, 1.21, 1.22, 1.22, 1.24, 1.3, 1.34, 1.36, 1.39, 1.44, 1.46, 1.53, 1.59, 1.6, 1.63, 1.68, 1.71, 1.72, 1.76, 1.83, 1.95, 1.96, 1.97, 2.02, 2.13, 2.15, 2.16, 2.22, 2.3, 2.31, 2.4, 2.45, 2.51, 2.53, 2.54, 2.78, 2.93, 3.27, 3.42, 3.47, 3.61, 4.02, 4.32, 4.58, 5.55, 2.54, 0.77.
Data 11: This data set represents the lifetime data relating to relief times (in minutes) of 20 patients receiving an analgesic and reported by Gross and Clark. The data are as follows: 1.1,1.4,1.3,1. 7,1.9,1.8,1.6,2.2,1.7,2.7,4.1,1.8,1.5,1.2,1.4,3.0,1.7,2.3,1.6,2.0.
From (Tables 1,2), it has been seen that theSauleh distribution have the smaller AIC, AICC and BIC values as compared to Parnav, Akash, Ishita and Lindley distribution. Hence we can concluded that the Sauleh distribution leads to a improved fit than other candidates models.
Table 1: MLE’s and Comparison Criterion.

Table 2: MLE’s and Comparison Criterion.

Acknowledgement
None
Conflict of Interest
No conflict of interest.
References
- Lindley DV (1958) Fiducial distribution and Bayes theorem. Journal of the Royal statistical society, series B 20(1): 102-107.
- Ghitny ME, Atieh B, Nadarajah S (2008) Lindley distribution and its Applications, Mathematics Computing and Simulation 78: 493-506.
- Shanker R (2015) Akash distribution and its Applications, International Journal of Probability and Statistics 4(3): 65-75.
- Shanker R (2015) Shanker distribution and its Applications, International journal of statistics and Applications 5(6): 338-348.
- Shanker R , Hagos F, Sujatha S (2015) on modeling of life time data using exponential and Lindley distributions, Biometrics and Biostatistics International Journal 3(2): 1-10.
- Shanker R, Shukla KK (2017) Ishita distribution and its Applications, BBIJ 5(2): 1-9.
- KK Shukla (2018) Pranav distribution with properties and applications, BBIJ 7(3): 244-254.
- Bjerkedal T (1960) Acquisition of resistance in guinea pigs infected with different doses of virulent tubercle bacilli. American Journal of Epidemiol 72(1): 130-148.
- Bonferroni CE Elementi di Statistica, Seeber,Firenze (1930) Soft Computing Applications for Group Decision-making and Consensus Modeling.
- Gross AJ, Clark VA (1975) Survival Distributions: Reliability Applications in the Biometrical Sciences, John Wiley, New York.
-
Ahmad Aijaz, Afaq ahmad, Rajnee tripathi. Sauleh Distribution with Statistical Properties and Applications. Annal Biostat & Biomed Appli. 4(1): 2020. ABBA.MS.ID.000581.
Incidence Rate; Index of Dispersion; Poisson Distribution; Odds Ratio; Restriction Level; Reduction Level; Tail Value at Risk; Vulnerability..
-

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
- Abstract
- Introduction
- Moments of Sauleh Distribution
- Skewness and Kurtosis of Sauleh Distribution
- Moment Generating Function of Sauleh Distribution
- Mean Deviation of Sauleh Distribution
- Mean Deviation From Median
- Bonferroni and Lorenz Curves
- Reliability Analysis
- Order Statistics
- Estimation of Parameters of Sauleh Distribution
- Data Analysis
- Acknowledgement
- Conflict of Interest
- References






