Analytical Investigations of the Performances and Effects of Heat Transfer Processes in Oscillatory Flow

Non-Newtonian fluid flow together with heat transfer and oscillation amid others has established the researchers’ interest in modern age as they are taking interest due to its extensive and widespread applications like in pollution like pollution control equipment’s, air-conditioning equipment’s, heating & ventilation systems, breathing aids, heat-lungs machines and other nano-fluids are examples. Numerous scientists and engineers have gone through and scrutinized this concept from innumerable rheological viewpoints. A fluid is a non-Newtonian liquid with exceptional features. Scientists have been successfully applied to a number of nonlinear problems arising in the science and engineering by various researchers like Khan et al. [1-2] discussed flow between rotating stretchable disks. rotating stretchable disks. What’s more, Khan et.al [1], found that when both the discs rotate in the same sense then the fluid in the disks rotates with an angular velocity. Khan et al. [3] discussed Dynamics with Cattaneo–Christov heat and mass flux theory of bioconvection Oldroyd- B nanofluid. Notwithstanding, Khan et al. [1-3] further ex plored that their study provides the best solutions and it has been proved that its solution is close to exact solution.

Khan et al. [4] discussed Rotating flow assessment of mag netized mixture fluid suspended with hybrid nanoparticles and chemical reactions of species. Rasheed et al. [5] discussed Computational analysis of hydromagnetic boundary layer stagnation point flow of nano liquid by a stretched heated surface with convective conditions and radiation effect. To this end, Mohmand et al. [25- 28] scrutinized oscillating and porous, and flow with heat transfer effect as well as vibratory flow. Usman et al.[6] discussed Computational optimization for the deposition of bioconvection thin Oldroyd- B nanofluid with entropy generation. Khan et al. [7] explored. Lorentz forces effects on the interactions of nanoparticles in emerging mechanisms with innovative approach. Khan et al. [8] analyzed Solution of magnetohydrodynamic flow and heat transfer of radiative viscoelastic fluid with temperature dependent viscosity in wire coating analysis. Khan et al. [9] investigated A Framework for the Magnetic Dipole Effect on the Thixotropic Nanofluid Flow Past a Continuous Curved Stretched Surface. Khan et al. [10] studied Analytical solution of UCM viscoelastic liquid with slip condition and heat flux over stretching sheet: Galerkin Approach.

Khan et al. [11] discussed Mechanical aspects of Maxwell nanofluid in dynamic system with irreversible analysis. Khan et al. [12] studied Numerical simulation of double-layer optical fiber coating using Oldroyd 8-constant fluid as a coating material. Shah et al. [13] analyzed Gravity Driven Flow of an Unsteady Second Order Fluid as well as Heat transfer rate of the fluid at the belt is also calculated. Khan et al. [14] discussed Investigation of wire coating using hydromagnetic third-grade liquid for coating along with Hall current and porous medium. Khan et al. [15] studied Analytical Solution of the MHD Viscous Flow over a Stretching Sheet by Multistep Optimal Homotropy Asymptotic Method. Fiza et al. [16] explored Modifications of the multistep optimal homotropy asymptotic method to some nonlinear KdV equations. Shah et al. [17] discussed The ADM solution of MHD non-Newtonian fluid with transient flow and heat transfer. Shah et al. [18] studied the Heat transfer and hydromagnetic effects on the unsteady thin film flow of Oldroyd-B fluid over an oscillating moving vertical plate.

Shah et al. [19]. explored for Soret and Dufour effect on the thin film flow over an unsteady stretching surface. Khan et al. [20] discussed for Mechanical aspects of Maxwell nanofluid in dynamic system with irreversible analysis as well as the impact of emerging parameters involved in the solutions are discussed through graphs on the velocity and temperature profiles in detail. Khan et al. [21] researched on the investigation of Wire Coating using Hydromagnetic Third-Grade Liquid for Coating along with Hall Current. Khan et al. [22] discussed the Analytical Solution of UCM Viscoelastic Liquid with Slip Condition and Heat Flux over Stretching Sheet: The Galerkin Approach. Mohmand et al. [23] discussed the Engineering Investigations of Dufour and Soret effect on MHD heat and mass transfer with radiative heat flux in a liquid over a rotating dick. Mohmand et al. [24] explored the Engineering applications and analysis of vibratory motion fourth order fluid film over the time dependent heated flat plate. Mohmand et al. [25] analyzed for Time dependent Oldroyd-B liquid film flow over an oscillating and porous vertical plate with the effect of thermal radiation. Mohmand et al. [26] studied Time dependent second grade fluid between two vertical oscillating plates with heat transfer effect. Mohmand et al. [27] investigated the Vibratory motion of fourth order fluid film over an unsteady heated flat. Mohmand et al. [28] discussed Engineering applications and analysis of vibratory motion fourth order fluid film over the time dependent heated flat plate. Mohmand et al. [29] explored for Heat transfer and hydromagnetic effects on the unsteady thin film flow of Oldroyd-B fluid over an oscillating moving vertical plate. Shah et al. [30] discussed Soret and dufour effect on the thin film flow over an unsteady stretching surface. Rasheed et al. [31] have discussed fluid flow through shooting technique and numerical approach. Moreover, Rasheed et al. [32 & 33] have discussed the fluid flow. Shah et al. [34] have also discussed MHD flow. Shah et al. [35] have scrutinized a mathematical and computational analysis of MHD fluid with heat source effect and the chemically reactive Casson fluid to add knowledge to the existing one. OHAM technique was also applied by Shah et al. [36]. Shah [37] has discussed analytical investigations of the performances and effects of heat transfer processes in oscillatory flow. Likewise Shah [38] has discussed Hugging flow through the powerful HAM technique. And as a concern of PDE or ODE was discussed by Khan et al. [39].

Shah et al. [17-19] have explored the transient flow, with unsteady stretching surface and accompanied by Soret and Dufour effects by the use of well-explanatory mathematical graphs. Khan et al. [8,10, & 12] have also discussed heat and heat transfer through mathematical graphs. Shah et al. [17-19] have investigated the behavior through graphical representation. Khan et al. [1-4] have discussed solution through of well-explanatory tables. Likewise Khan et.al, [20] have also discussed about the Brownian motion and thermophoresis with thermal radiation through mathematical graphs. The oscillating parallel plates were discussed by Shah et al. [13] through mathematical graphs. Similarly, Fiza et al. [16] have discussed flow through numerical results (Runge-Kutta method) and graphical language. Moreover, flow of Oldroyd-B fluid over an oscillating was discussed by Shah et al. [29] through an interesting graphical representation. Likewise Mohmand et al. [28] have discussed time-dependent heated plate by determining their graphs. To this end, Khan et.al. [2] have investigated pressure distribution and entropy generation rate and then their solution through HAM approach and then exposed the results by coloured graphical language. Moreover, Khan et.al. [3-5] Darcy–Forchheimer law is used to study heat and mass transfer flow and micro-organisms motion in porous media as well as flow of Maxwell nanofluid induced by two parallel rotating disks were analyzed and discussed the intriguing results through statisical tables. Furthermore Rasheed et al. [31-33] have discussed fluid motion of fluid analysis through mathematical graphs. Khan et al. [1-4] have analyzed the fluid motion through statisical tables and graphs. Similarly, Shah et al. [17- 19] have also investigated the MHD fluid motion through coloured graphs which gets a superb accord with the previous online available work. Likewise, Khan et al. [7-12] have also discussed fluid flow through interesting statistical tables as well as mathematical graphs and found excellent harmony with the already published work. Similarly Usman et al. [6] discussed Computational optimization through mathematical graphs. Moreover, Fiza et al. [15 & 16] have discussed the analytical solution of the MHD and Modification of the OHAM solution through mathematical graphs and statistical tables. What’s more, Shah et al. [34-38] have also put enough commentary to portray and display different fluids behaviors through mathematical graphs as well as statistical tables..The author’s goal in this study is to examine the non-Newtonian fluid model, which includes two-dimensional fluid flow of a viscous, incompressible, and electrically conducting fluid in two parallel plates, and to represent the obtained results in graphical as well as in a tabulated form.

We know that,

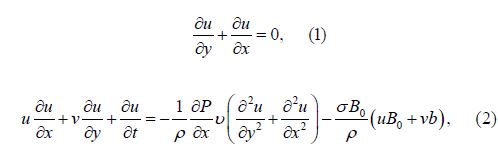
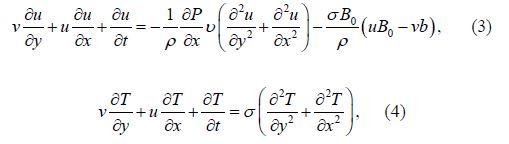
The Reynolds number is calculated from the equations;

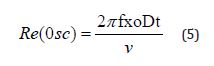
In this equation, f represents the oscillatory frequency; xo stands for the highest level of oscillation and Dt represents the tube diameter while v is the velocity of the cooling fluid used in the oscillatory heat pipe. The Strophe number equation is used as the definitive measure of the outcomes of the oscillatory amplitude, which means that its value is inversely proportional to it.

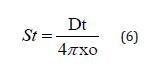
The above equations (5) and (6) are used to measure the overall effectiveness of the oscillatory heat pipe and to determine the net flow of particles within the convection current, which represents heat transfer across the system. Mixing of fluids in the baffle region depends on the processes by which vortices form, their enlargement, and how they interact with each other, a feature that enables heat interchange between the walls of the tube and the rest of the fluid. Oscillatory flow employing the batch principle achieves high levels of heat transfer with significantly greater energy efficiency than turbulent pipes and stirred tanks. A heat transfer coefficient varies with the force of oscillation, with the amount of heat for which oscillation is expected to transport being directly proportional to the energy levels achievable. It can, therefore, be derived those oscillatory flows are more intense in areas where the temperatures of the high-temperature system are higher and less potent in zones of cooler temperatures.

Consider the flow of a thin film of fluid in inclined two plates. The thickness δ of the fluid is uniform. There is an external homogeneous magnetic field B applied to the plates. In problem, y-axis is perpendicular to the plates and x-axis is taken parallel to the surface and y-axis. Assume that the pressure is atmospheric and flow is lamina and unsteady. Then the velocity field is,

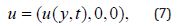
Subject to the following boundary conditions,

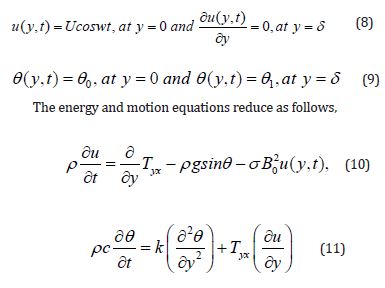
The component T_yx of the fluid is

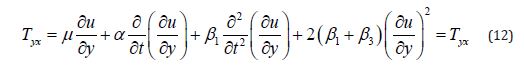
Using (12) in (10) and (11), we obtain as the following result,

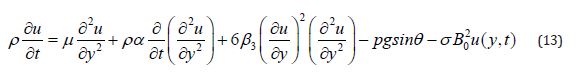
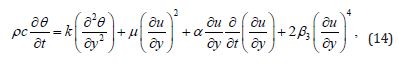
Introduce non-dimensional variables

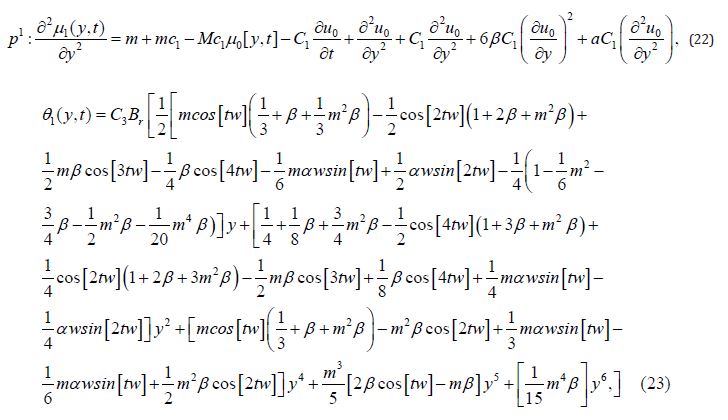
The solution of the second component of velocity distribution is too large. So, derivation is given up to first order while, graphical solutions are given up to second order. The value of Cj for the velocity components u0(y, t), u₁(y, t, c1), and _u2(y, t, c2) are c₁

c₂ =0.79699391, c₃ = 0.0009547247523, c₄ = - 0.005.

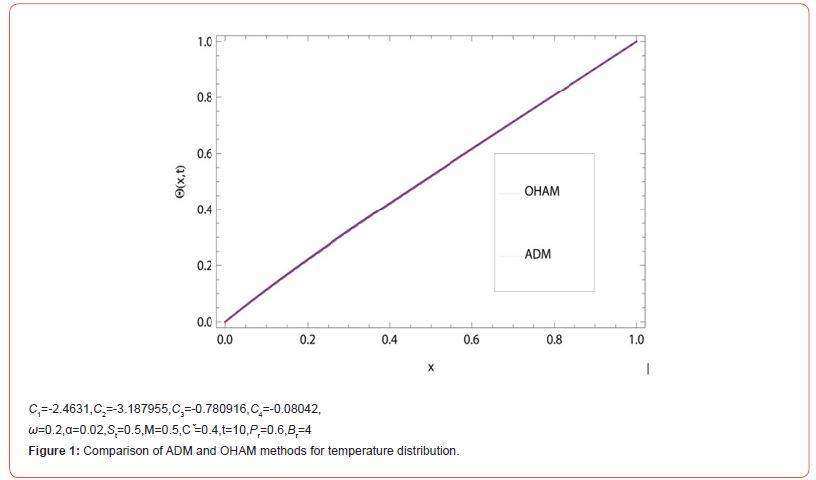
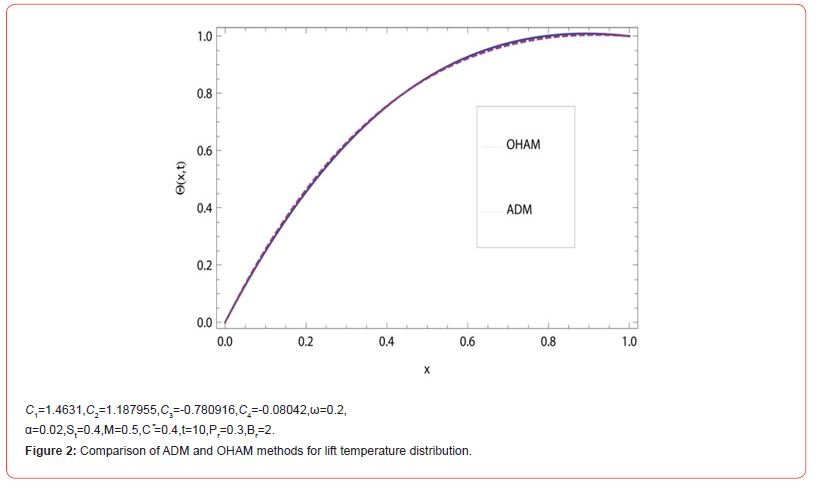
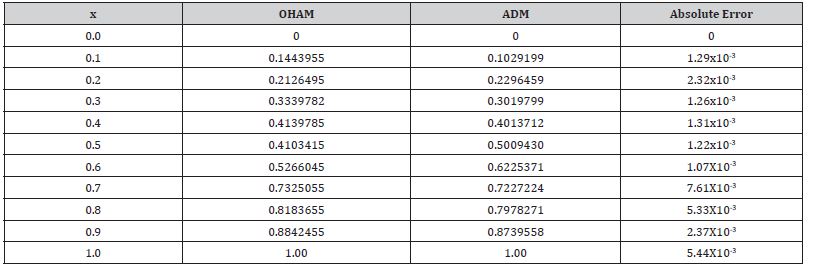
Comparison of OHAM and ADM

Table 1: Comparison of OHAM and ADM for drainage temperature distribution.

Conclusion

Oscillatory flows occur as a result of movement of fluid from one zone to another, where it encounters another fluid with different physical properties. Interactions between the fluids lead to an exchange of these physical properties, and the reversal of flow as the tangible property ultimately spreads along the whole section of the material. In oscillatory heat plates, the physical feature is heat. As the fluid travels through, the heat is transferred to other sections. Applications of oscillatory heat plates depend on this property of continual flow as long as heat levels remain different to facilitate an automatic cooling system. The comparison of OHAM and ADM has been inferred graphically and numerically. The impacts of physical parameters have been portrayed and examined. The findings suggest that oscillatory flows are accelerated by heat transfer processes, which in turn speeds up the transfer of heat from the point of high concentration to the point of low concentration.